알고리즘 - 시간 복잡도(Time Complexity)
이번 게시물은 시간 복잡도에 대해 정리해 보도록 하겠습니다.
정렬 알고리즘이나 백준 알고리즘을 풀 때도 사실 시간 복잡도를 고려하지 않을 수 없습니다.
백준 알고리즘 문제에 시간 복잡도라는 단계가 생긴 김에 미뤄 왔던 시간 복잡도 게시물을 한 번 작성하도록 해보겠습니다.
시간 복잡도란?
제작한 프로그램이 문제를 해결하는데 얼마나 많은 시간을 필요로 하는지 살펴보는 것을 말합니다.
알고리즘을 공부해 보신 분들이라면 알겠지만
어떠한 문제를 해결하기 위해서는 여러 가지 방법들이 존재합니다.
시간적인 측면으로만 봤을 때 가장 효율적인 방법을 찾을 때 기준이 되는 지표가 바로 시간 복잡도입니다.
시간 복잡도는 기본적으로 3가지 표기법을 가지고 있습니다.
Big-O (빅-오) - 상한 접근
Big-Ω (빅-오메가) - 하한 접근
Big-θ (빅-세타) - 그 둘의 평균
위에 3가지 내용에 대해서는 조금 뒤에 설명하도록 하고 시간 복잡도에 대해 근본적인 이야기를 해보도록 하겠습니다.
시간 복잡도를 어떤 식으로 계산할까요?
어떠한 프로그램이 실행되고 계산될 때 시간에 영향을 미치는 것이 무엇이 있을까요?
CUP 성능, 캐시 양, SSD, 그래픽 카드 등등.. 여러 가지 요인들이 있을 것입니다.
근데 개발자는 이런 하드웨어적인 부분을 다 고려해서 시간이 얼마나 걸리는지 측정하고 싶은 것이 아닙니다.
그저 내가 만든 프로그램이 얼마나 시간을 써야 문제 해결이 되는지가 궁금한 겁니다.
그래서 그것의 기준을 만들기 시작했습니다.
예를 들어 보겠습니다.(저자는 자바가 제일 익숙하기 때문에 자바로 코드 예시를 보여드리겠습니다.)
import java.text.SimpleDateFormat; public class Time_Complexity { public static void main(String[] args) { long time1 = System.currentTimeMillis();//시작 시간 time_complexity(1); long time2 = System.currentTimeMillis();//끝나는 시간 System.out.println(new SimpleDateFormat("yyyy-MM-dd HH:mm:ss:SSS").format(time1));//시작 시간 시간 포맷 System.out.println(new SimpleDateFormat("yyyy-MM-dd HH:mm:ss:SSS").format(time2));//시작 시간 시간 포맷 } //시간 측정 함수 public static void time_complexity(int n){ System.out.println(n); } }
뭔가 복잡한 게 많이 있지만 중요한 건 time_complexity 함수입니다.
함수 호출의 위아래로 있는 건 현 시간을 알려주는 구문입니다.
가장 밑에 출력을 통해 함수 시작과 끝의 시간을 구해 해당 함수가 얼마나 시간이 걸렸는지 알 수 있습니다.

시간을 보시면 1을 출력하는 데 0.001초 정보 소유가 되었다고 보시면 됩니다.
n에 100을 넣으면 어떻게 될까요?

n에 100을 넣어도 단 0.001초도 걸리지 않았습니다. 시간이 줄어든 이유는 이미 메모리에 올라갔기 때문에 시간이 좀 덜 걸린 게 아닌가 생각됩니다.
다음 예시를 보겠습니다.
import java.text.SimpleDateFormat; public class Time_Complexity { public static void main(String[] args) { long time1 = System.currentTimeMillis();//시작 시간 time_complexity(1); long time2 = System.currentTimeMillis();//끝나는 시간 System.out.println(new SimpleDateFormat("yyyy-MM-dd HH:mm:ss:SSS").format(time1));//시작 시간 시간 포맷 System.out.println(new SimpleDateFormat("yyyy-MM-dd HH:mm:ss:SSS").format(time2));//시작 시간 시간 포맷 } //시간 측정 함수 public static void time_complexity(int n){ for(int i=0; i<n; i++){ System.out.println(i); } } }
네, 이번에는 함수 안에 반복문을 넣어봤습니다. 그럼 상식상으로 코드가 반복되니 시간이 좀 더 들 것으로 예상됩니다.
n=1 일 때는 시간이 얼마나 걸릴까요?

역시 0.001초가 걸리는 것을 알 수 있습니다. 반복이 1번만 돌았으니 위에 시간과 동일하게 시간이 얼마 걸리지 않은 것을 알 수 있습니다. 그렇다면 n=100일 때도 마찬가지일까요?

네, 예상한 대로 0.006초 6배나 더 걸린 것을 알 수 있습니다.
실제 시간을 예측할 수 있는 시간 복잡도
위에서 보았듯이 각 프로그램은 걸리는 시간이 모두 다릅니다.
이것을 예측할 수 있는 것이 시간 복잡도입니다.
물론, 시간 복잡도로 정확히 걸리는 시간을 알 수는 없습니다.
위에서 말한 CUP 성능, 캐시 양, SSD, 그래픽 카드 등등.. 이유들 때문입니다.
하지만 프로그램 적으로 알고리즘이 얼마나 시간이 걸리는지 성능과 상관없이 순수한 알고리즘의 시간을 예측하기 위해 만들어진 것이 시간 복잡도입니다.
그래서 시간복잡도는 실행 시간으로 표현합니다.
실행 시간이란 함수/알고리즘에 수행에 필요한 스텝 수를 이야기합니다.
실행시간의 스텝 수
그렇다면 실행시간의 스텝 수를 어떻게 구할 수 있을까요?
예제 코드를 한번 보겠습니다.
//시간 측정 함수 public static void time_complexity(int n){ int count = 0; for(int i=0; i<n; i++){ count++; System.out.println(count); } }
스텝 수는 해당 라인이 얼마나 수행되는지를 수식으로 볼 수 있도록 한 것입니다.

위와 같이 해당 라인을 수행하는 시간을 C1, C2, C3, C4로 표현해 보도륵 하겠습니다.
그렇다면
C1 = 1
C2 = n+1(1이 추가된 이유는 루프를 탈출하기 위해 한 번을 더 반복하기 때문입니다.)
C3 = n
C4 = n
이렇게 표현되게 됩니다.
다음 수식은 아래와 같이 정리됩니다.
T(n) = (C1*1) + (C2*(n+1)) + (C3*n) + (C4*n)
T(n) = C1 + C2*n + C2 + n(C3+C4)
T(n) = n(C2+C3+C4) + C1 + C2
해당 C들은 스텝에 관한 수식임으로 모두 상수에 해당합니다.
즉, T(n) = an+b형태의 수식을 가지게 됩니다.
여기서 우리가 알고 싶은 내용은 n=∞ 일 때입니다.
n의 숫자가 작으면 어차피 빨리 끝나게 될 테니깐요.
그래서 n=∞ 일 때 어떤 현상이 일어나는지를 좀 더 쉽게 나타내기 위해 점근적 분석을 하게 됩니다.
점근적 분석, 점근적 표기법
점근적 분석은 n이 커질 때 무의미한 상수와 최고차항의 계수를 제거해 주는 것을 말합니다.
위에 수식을 다시 보면
T(n) = an+b 형태에서 그냥 n으로 수식을 보는 것을 점근적 분석이라고 하는 것이죠.
여기서 더 나아가서 O(n), 𝚹(N),Ω(n) 등으로 표현하는 것을 점근적 표기법이라고 합니다.
상한선과 하한선에 따른 시간 복잡도
예제를 하나 더 보도록 하겠습니다.
public static boolean time_complexity(int[] array, int num){ for(int i=0; i<array.length; i++){ if(array[i] == num){ return true; } } return false; }
다음 함수는 배열 안에 있는 수를 비교해 해당 수와 같으면 true를 반환하고 없으면 false를 반환하는 함수입니다.
해당 함수는 찾고자 하는 번호가 앞에 있으면 빨리 종료될 것이고 뒤에 있으면 늦게 종료될 것입니다.
해당 함수는 어떻게 시간복잡도를 표현할 수 있을까요?
best case와 worst case로 나눠서 표현해 보도록 하겠습니다.
best case : 찾고자 하는 번호가 맨 앞에 있을 때 -> 배열의 길이와 상관없이 항상 상수만큼 일정한 시간이 걸림
worst case : 찾고자 하는 번호가 맨 뒤에 있을 때 -> 배열의 길이 n만큼의 시간이 걸림
그래프 관점으로 보면
해당 시간 복잡도는
함수 실행 시간은 아무리 빨라도 상수 시간 이상입니다 : 하한선(lower bound)을 기준으로 서술
함수 실행 시간은 아무리 오래 걸려도 N에 비례하는 정도 이하입니다 : 하한선(lower bound)을 기준으로 서술
해당 시간 복잡도를 기호를 나타내면
𝝮(1)
O(N)
가 됩니다.
여기서 𝝮(big omega)는 lower bound를 의미하고요, O(big Oh)는 upper bound를 의미합니다. 𝝮(1)의 1이 의미하는 것은 상수(constant)를 의미합니다. O(N)의 N이 의미하는 것은 배열의 크기를 의미합니다.
보통 일반적으로 하한선보다는 상한선을 더 궁금해하기 때문에 주로 O(N)을 많이 쓴다고 볼 수 있겠습니다.
빅 오(Big-O) 표기법의 종류
1. O(1)
2. O(n)
3. O(log n)
4. O(n2)
5. O(2n)
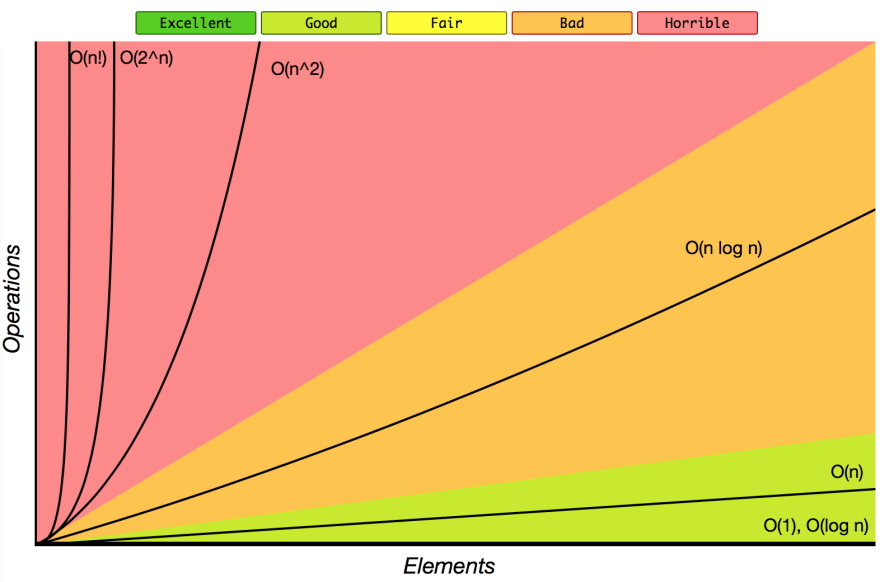
1. O(1)
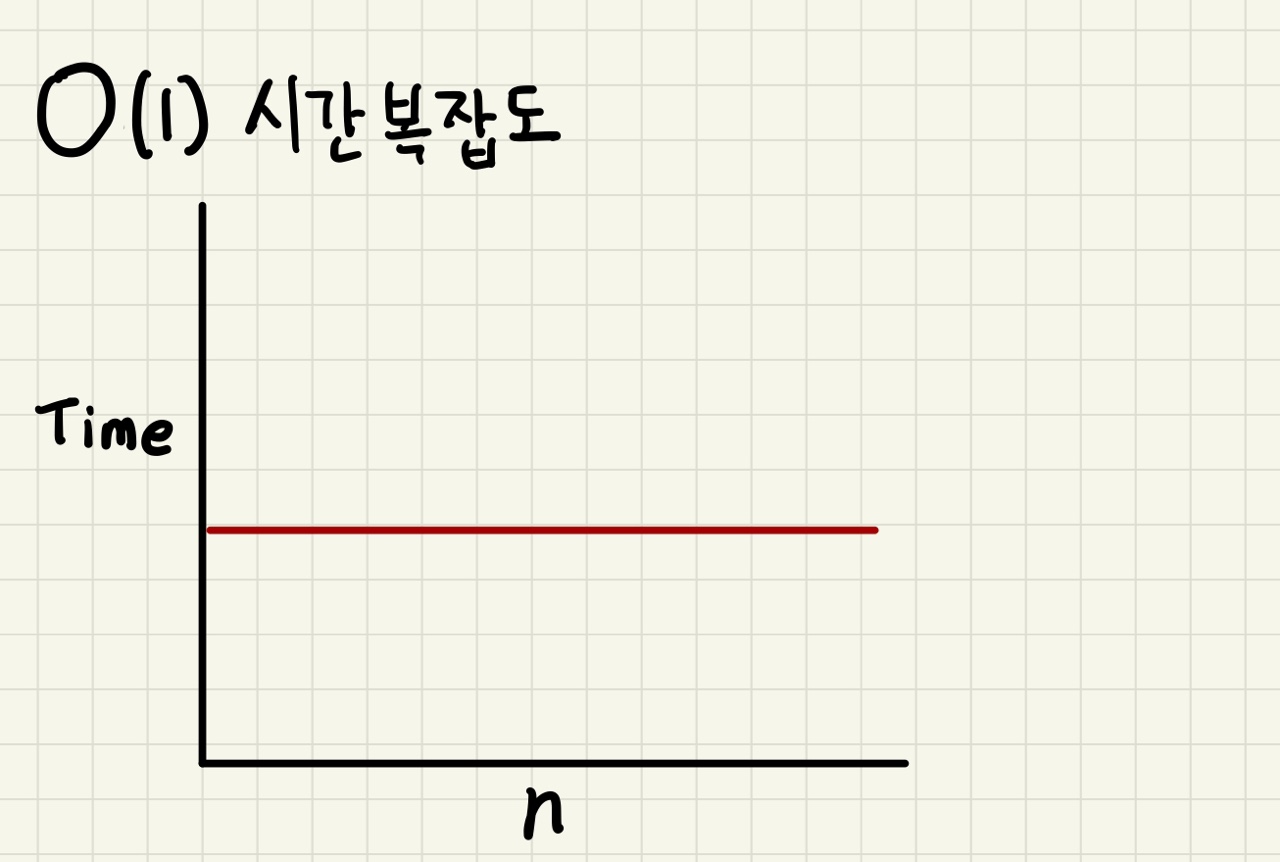
일정한 시간복잡도라고라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않습니다.
O(1)의 시간복잡도를 가진 알고리즘
import java.text.SimpleDateFormat; public class Time_Complexity { public static void main(String[] args) { int[] array = new int[10]; for(int i=0; i<10; i++){ array[i] = (int)(Math.random()*100); } int result = time_complexity(array, 1); System.out.println(result); } public static int time_complexity(int[] array, int n){ return array[1]; } }
2. O(n)
- O(n)은 선형 복잡도라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미합니다.
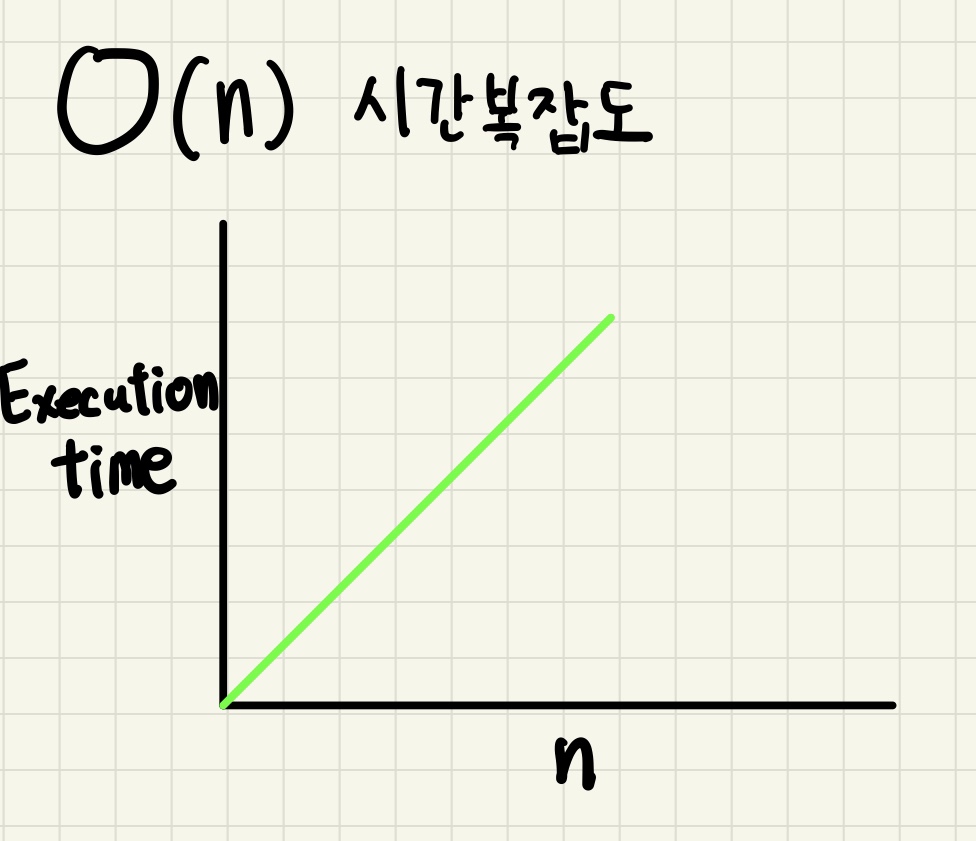
O(n)의 시간복잡도를 가진 알고리즘
import java.text.SimpleDateFormat; public class Time_Complexity { public static void main(String[] args) { int[] array = new int[10]; for(int i=0; i<10; i++){ array[i] = (int)(Math.random()*100); } time_complexity(10); } public static void time_complexity(int n){ for(int i=0; i<2*n; i++){ System.out.println(i); } } }
- 해당 코드를 보시면 n의 2배만큼 반복문이 진행되어 n의 2배 즉, 2n의 시간 복잡도가 걸릴 것으로 예상됩니다.
하지만 O(2n)으로 표기하지 않습니다. 이유는 점근적 표기법으로 최고차항의 계수를 제거하고 표기하기 때문입니다.
그래서 O(n)으로 표기합니다.
3. O(log n)
- O(log n)은 로그 복잡도(logarithmic complexity)라고 부르며, Big-O표기법 중 O(1) 다음으로 빠른 시간 복잡도를 가집니다.
- O(log n)은 대표적으로 BST 탐색 기법이 있습니다.
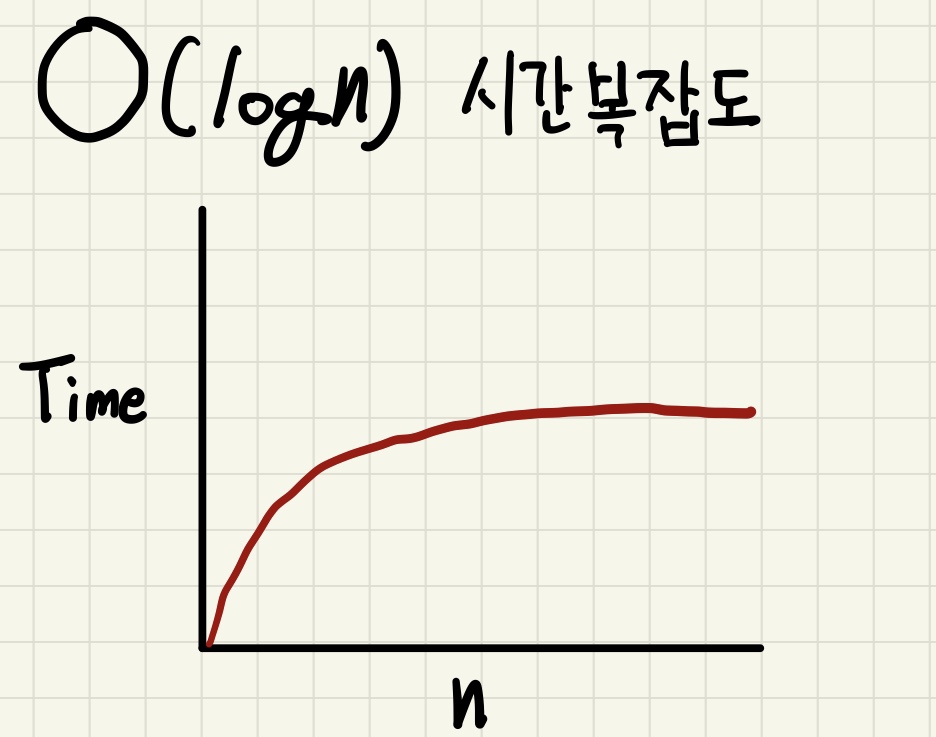
4. O(n2)
- O(n2)은 2차 복잡도라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미합니다.
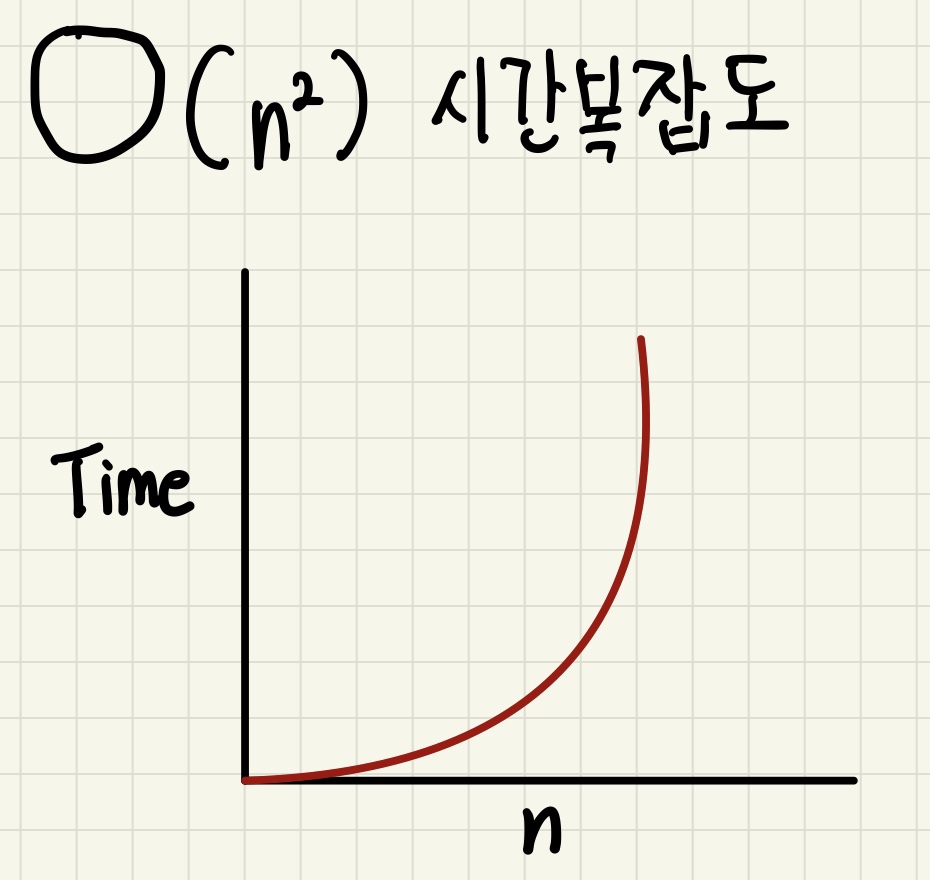
O(n2)의 시간복잡도를 가진 알고리즘
import java.text.SimpleDateFormat; public class Time_Complexity { public static void main(String[] args) { int[] array = new int[10]; for(int i=0; i<10; i++){ array[i] = (int)(Math.random()*100); } time_complexity(10); } public static void time_complexity(int n){ for(int i=0; i<n; i++){ for(int j=0; j<n; j++){ for(int a=0; a<n; a++){ System.out.println(a); } } } } }
- 해당 코드를 보시면 n3이라고 생각하실 수 있지만 이 역시 점근적 표현법으로 뒤로 갈수록 제곱의 영향의 차이가 미미해지기 때문에 O(n2)라고 표기합니다.
4. O(2n)
- O(2n)은 기하급수적 복잡도라고 부르며, Big-O 표기법 중 가장 느린 시간 복잡도를 가집니다.
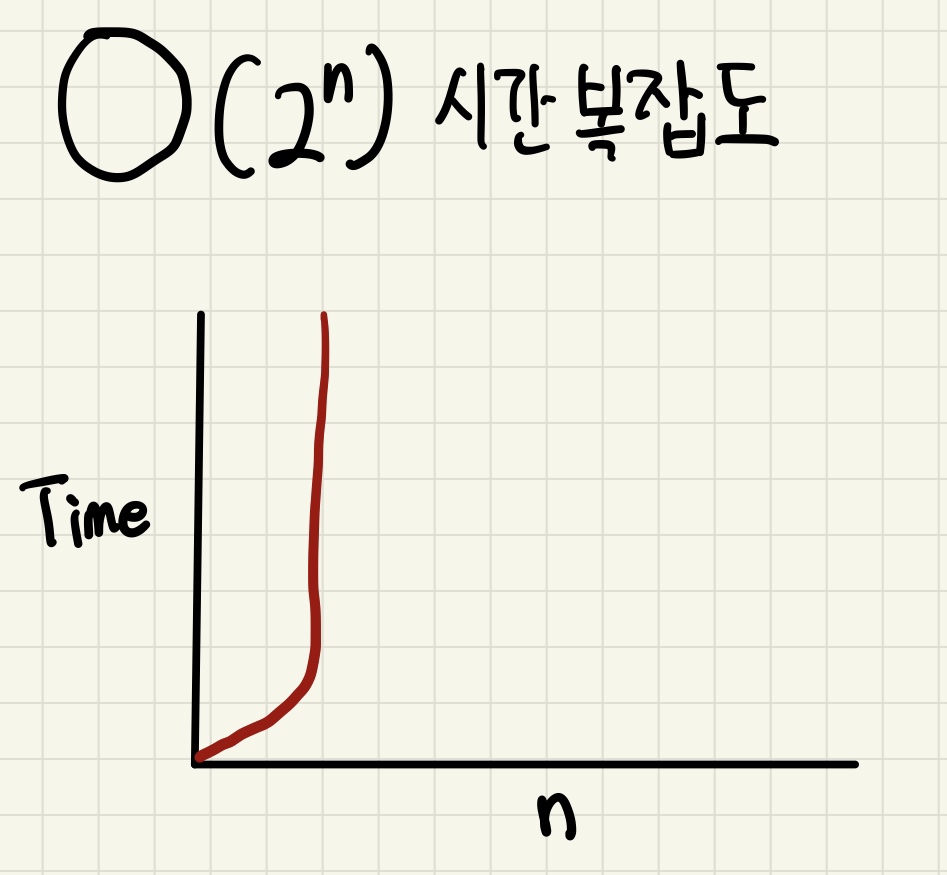
O(2n)의 시간복잡도를 가진 알고리즘
import java.text.SimpleDateFormat; public class Time_Complexity { public static void main(String[] args) { System.out.println(time_complexity(9)); } public static int time_complexity(int n){ if(n<=1){ return 1; } return time_complexity(n-1) + time_complexity(n-2); } }
- 피보나치 재귀 수열로 대표적인 O(2n)의 시간복잡도를 가지는 알고리즘입니다.
참고
[알고리즘] Time Complexity (시간 복잡도) - 하나몬
⚡️ Time Complexity (시간 복잡도) Time Complexity (시간 복잡도)를 고려한 효율적인 알고리즘 구현 방법에 대한 고민과 Big-O 표기법을 이용해 시간 복잡도를 나타내는 방법에 대해 알아봅시다. ❗️효
hanamon.kr
https://blog.chulgil.me/algorithm/
알고리즘의 시간 복잡도와 Big-O 쉽게 이해하기
삼성역에서 택시를 타고 강남역으로 향했는데 30분 걸렸다. 구글에서 알려주는 최단경로로 갔더라면 15분내에 도착할 것이다. 레스토랑을 예약해서 가는 경우라던지 친구와 약속시간을 잡은경
blog.chulgil.me
https://namu.wiki/w/%EC%8B%9C%EA%B0%84%20%EB%B3%B5%EC%9E%A1%EB%8F%84
시간 복잡도 - 나무위키
이 저작물은 CC BY-NC-SA 2.0 KR에 따라 이용할 수 있습니다. (단, 라이선스가 명시된 일부 문서 및 삽화 제외) 기여하신 문서의 저작권은 각 기여자에게 있으며, 각 기여자는 기여하신 부분의 저작권
namu.wiki
https://ko.wikipedia.org/wiki/%EC%8B%9C%EA%B0%84_%EB%B3%B5%EC%9E%A1%EB%8F%84
시간 복잡도 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 러닝 타임은 여기로 연결됩니다. 매체의 재생·상영 시간에 대해서는 러닝 타임 (매체) 문서를 참고하십시오. 계산 복잡도 이론에서 시간 복잡도는 문제를 해결
ko.wikipedia.org
https://terms.naver.com/entry.naver?docId=3609919&cid=58598&categoryId=59316
시간 복잡도
알고리즘이 어떤 문제를 해결하는데 걸리는 시간. 좋은 프로그램을 선별하는 기준 중 하나인 시간복잡도는 제작한 프로그램이 문제를 해결하는데 얼마나 많은 시간을 필요로 하는지 살펴보는
terms.naver.com
https://www.youtube.com/watch?v=tTFoClBZutw&t=526s
https://hudi.blog/time-complexity/
[ALG] 시간복잡도와 빅오 (Big-O) 표기법
본 포스트는 저자가 학습하며 작성한 글 이기 때문에 틀린 내용이 있을 수 있습니다. 지적은 언제나 환영입니다. 1. 알고리즘의 비용 계산 특정 문제를 해결하는 알고리즘은 여러가지가 존재할
hudi.blog
https://easy-code-yo.tistory.com/13
시간복잡도 개념, Big-O(빅 오) 표기법, 점근적 표기법 설명
영상 내용을 글로도 정리했습니다 아주 아주 쉽게 설명합니다 :) 예제로 알아보는 시간 복잡도(time complexity) 개념 아래와 같은 코드가 있습니다. 이 코드는 정수 타입의 배열 inputs과 multiplier를 파
easy-code-yo.tistory.com
댓글을 사용할 수 없습니다.