자바로 구현한 합병 정렬(병합 정렬) 알고리즘 - 분할 정복
목차
1. 합병 정렬에 관하여
합병 정렬 알고리즘은 정렬 알고리즘의 하나로 분할 정복을 사용한 알고리즘입니다.
합병 정렬의 특징으로는 1. 비교 정렬입니다. 2. 제자리 정렬이 아닙니다. 3. 안정정렬입니다.
1. 비교 정렬 : 서로 값을 비교하여 정렬하는 알고리즘입니다.
2. 제자리 정렬 : 해당 배열 외에 또 다른 배열의 저장 공간이 필요가 없습니다.
3. 안정정렬 : 같은 값일 경우 해당 정렬이 변경되지 않습니다.
2. 분할 정복 알고리즘에 관하여
그럼 분할 정복이 무엇인지 알아보겠습니다.
분할 정복은 커다란 문제를 나눌 수 있는 가장 작은 단위까지 나누어 해결한 후에 그 결과 값을 조합함으로 문제를 해결하는 알고리즘입니다.
말로 하면 어려울 수 있으니 그림을 보겠습니다.

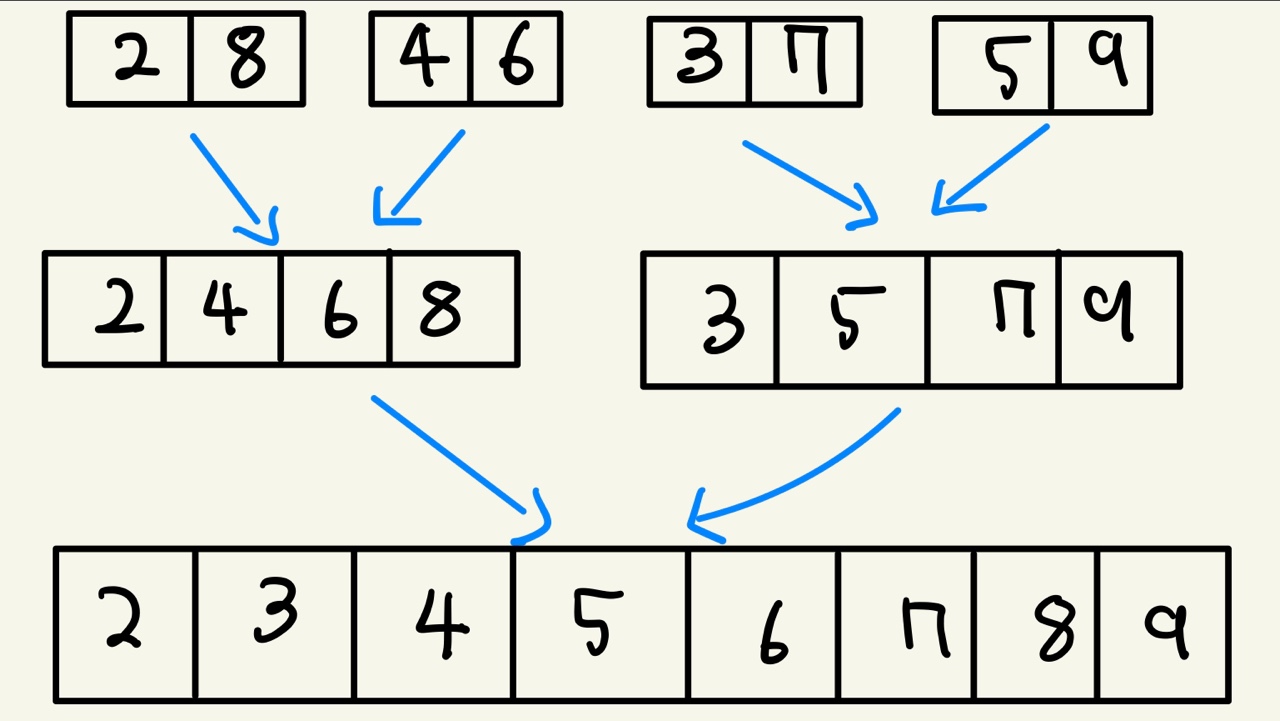
위 그림을 보시면 먼저 [8,2,6,4,7,4,9,5]라는 list가 있습니다. 이 배열을 낮은 순서대로 정렬을 하는 것이 목적입니다.
분할 정복 알고리즘을 사용하여 해당 문제를 해결하기 위해서는 list의 길이가 1인 서브 리스트까지 쪼개주어야 합니다.
위에 그림의 8,2,6,4,7,4,9,5 가 모두 따로 쪼개져 있는 것을 알 수 있습니다. 그 후에 파란색 화살표부터 비교하면서 조합해 줍니다. 8,2를 6,4를 7,4,를 9,5를 비교하여 정렬해 줍니다. 그 후에 다시 정렬된 상태의 길이가 2인 서브 리스트를 비교하여 정렬해 줍니다. 2,8,4,6을 3,7,5,9를 비교하여 정렬해 줍니다. 그 후에 역시 다음을 똑같이 병합합니다. 2,4,6,8,3,5,7,9를 정렬해서 정렬을 완료해 줍니다.
3. 병합 정렬 알고리즘 로직과 질문
해당 과정을 요약하면 다음과 같습니다.
1. 주어진 리스트를 절반으로 분할하여 부분리스트를 만든다.
2. 해당 부분 리스트 길이가 1이 아니라면 1번 과정을 되풀이한다.
3. 인접한 부분리스트끼리 정렬하여 합친다.
그럼 2가지 질문이 생길 수 있습니다.
1. 어차피 정렬을 합치면서 계속 비교해 주는데 한 번에 전체 정렬하는 게 훨씬 효율적이지 않나요?
2. 그럼 절반으로 쪼개지지 않는 리스트 길이가 7개나 9개는 사용할 수 없는 알고리즘인가요?
1. 어차피 정렬을 합치면서 계속 비교해 주는데 한 번에 전체 정렬하는 게 훨씬 효율적이지 않나요?
아닙니다. 뒤에서 코드 구현을 하면서 다시 한번 이야기하겠지만 서브 리스트가 이미 정렬되어 있는 상태이기 때문에 정렬을 훨씬 효율적으로 할 수 있습니다.
예를 들어 1,4,5,6과 3,7,8,9를 합치는 과정이라고 생각해 봅시다
1(왼쪽 서브리스트의 첫 번째 리스트)과 3(오른쪽 서브리스트의 첫 번째 리스트)을 비교해서 1을 입력하고
4(왼쪽 서브리스트의 두 번째 리스트)와 3(오른쪽 서브리스트의 첫 번째 리스트)을 비교해서 3을 입력하고
4(왼쪽 서브리스트의 두 번째 리스트)와 7(오른쪽 서브리스트의 두 번째 리스트)을 비교해서 4를 입력하고
5(왼쪽 서브리스트의 세 번째 리스트)와 7(오른쪽 서브리스트의 두 번째 리스트)을 비교해서 5를 입력하고
6(왼쪽 서브리스트의 네 번째 리스트)과 7(오른쪽 서브리스트의 두 번째 리스트)을 비교해서 6을 입력합니다.
그렇게 되면 [1,3,4,5,6]이 정렬이 되었고 왼쪽의 서브리스트[1,4,5,6]는 모두 정렬된 상태로 끝이 났고 오른쪽의 서브 리스트[3,7,8,9]는 3을 제외하고는 입력되지 못했습니다.
7,8,9는 이미 정렬되어 있는 상태이므로 [1,3,4,5,6] 리스트 뒤에 그냥 붙이기만 하면 정렬이 완성되는 것입니다.
이런 형태로 코드가 진행되기 때문에 이미 정렬된 상태의 서브리스트를 합치는 것은 매우 효율적인 방법인 것입니다.
2. 그럼 절반으로 쪼개지지 않는 리스트 길이가 7개나 9개는 사용할 수 없는 알고리즘인가요?
아닙니다. 9개일 경우 0~4,5~8로 나누고 5~8을 5~6,8로 나눈 후에 다시 병합하는 형식으로 합니다. 병합하는 과정도 나눌 때와 똑같이 반대로 올라간다고 생각하시면 됩니다. 자세한 내용은 구현하면서 설명해 드리겠습니다.
4. 병합 정렬 알고리즘 자바 구현
병합 정렬은 2가지 방법으로 나눠집니다.
1. [TOP-DOWN] 형식
2. [BOTTOM-UP] 형식
먼저 [TOP-DOWN] 형식을 보겠습니다.
[TOP-DOWN] 전체코드
import java.util.Scanner;
public class Merge_sort {
static int[] sort_array;// 새로운 정렬을 저장할 배열
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
//배열의 길이를 결정
int array_length = sc.nextInt();
int[] array = new int[array_length];//초기 배열
sort_array = new int[array_length];//정렬을 저장할 배열
//배열 초기화
for(int i=0; i<array.length; i++){
array[i] = (int)(Math.random()*100);
}
//정렬 하기 전 배열 출력
for(int i=0; i<array.length; i++){
System.out.printf("%d ",array[i]);
if((i+1)%10 == 0){
System.out.println();
}
}
//합병 정렬 함수
merge_sort(array,0,array_length-1);
System.out.println();
System.out.println();
//정렬 후 병열 출력
for(int i=0; i<array.length; i++){
System.out.printf("%d ",array[i]);
if((i+1)%10 == 0){
System.out.println();
}
}
}
/*
* [TO-DOWN] 방식
* 위에서 부터 아래로 내려가는 합병 정렬 방식으로
* 재귀 함수를 통해 길이가 1인 서브리스트가 될때까지 쪼개준 후에
* 합치는 과정에서 merge함수를 실행한다.
*/
public static void merge_sort(int[] array, int first, int second){
/*
* 재귀 함수의 경우 무한 루프를 탈 수 있기 때문제 조건부 return을 꼭 걸어줘야 한다.
* 해당 반환은 첫번쨰값과 두번째 값이 같을 때 반환을 하는데
* 이는 서브 리스트 길이가 1임을 의미한다
*/
if(first == second) return;
//반인 인덱스를 찾는 mid 변수
int mid = (first+second)/2;
/*
* 첫번째 값과 mid값(반값)을 재귀 함으로 인데스를 반으로 나눌 수 있게 된다.
* 위에는 왼쪽의 서브 리스트 아래 함수는 오른쪽의 서브 리스트를 의미한다.
*/
merge_sort(array,first,mid);
merge_sort(array,mid+1,second);
/*
* 재귀가 끝나고 merge함수가 실행되었다는 의미는
* 차례되로 반환되어 병합하고 있다는 의미이다.
* 그럼으로 병합 함수를 실행한다.
*/
merge(array,first,mid,second);
}
public static void merge(int[] array, int first, int mid, int second){
int l = first;//왼쪽의 비교할 서브 리스트의 인덱스
int m = mid+1;//오른쪽의 비교할 서브 리스트의 인덱스
int index = first;//비교 한 후 입력할 배열
//외쪽과 오른쪽 둘 중 하나의 서브 리스트의 비교가 끝나면 while문을 종료합니다.
while(l<=mid && m<=second){
//왼쪽 서브리스트와 오른쪽 서브 리스트를 비교하면서 정렬 배열에 입력합니다.
if(array[l] <= array[m]){
sort_array[index] = array[l];
l++;
index++;
}
else{
sort_array[index] = array[m];
m++;
index++;
}
}
/*
* 왼쪽 서브 리스트와 오른쪽 서브 리스트가 정렬 배열에 입력되지 않고 남았을경우
* 이미 서브 리스트는 정렬이 되어 있는 상태임으로 정렬된 리스트 뒤에 붙입니다.
*/
while(l<=mid){
sort_array[index] = array[l];
l++;
index++;
}
while(m<=second){
sort_array[index] = array[m];
m++;
index++;
}
//정렬된 배열의 값을 배열에 입력합니다.
for(int i=first; i<=second; i++){
array[i] = sort_array[i];
}
}
}
구현에 대한 이야기를 한번 해보겠습니다.
구현이란 내 머릿속에 있는 로직 혹은 알고리즘을 코드로 현실화하는 것을 말합니다.
이것을 잘하는 사람이 개발을 잘한다고 말할 수 있겠죠
정렬 알고리즘은 구현이 쉽지가 않습니다.
어느 정도 가닥이 있으신 분들은 전체코드의 주석만 보셔도 괜찮습니다.
하지만 처음 알고리즘을 공부하시는 분들이라면 하나하나 차근차근 밟아가다 보면 정답을 보지 않아도 해당 로직을 구현할 수 있는 능력이 생기게 됩니다.
믿고 구현 내용을 한번 살펴보겠습니다.
먼저 main 함수 부분입니다. 이 부분은 배열을 생성하고 출력하는 역할을 합니다.
main 함수 위에 sort_array로 정렬 후 담을 배열이 선언되어 있는데 전역으로 선언한 이유는 매개변수로 쓰기 귀찮고 함수를 실행할 때마다 새로 메모리를 만들게 되면 자원이 낭비되기 때문입니다.
static int[] sort_array;// 새로운 정렬을 저장할 배열
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
//배열의 길이를 결정
int array_length = sc.nextInt();
int[] array = new int[array_length];//초기 배열
sort_array = new int[array_length];//정렬을 저장할 배열
//배열 초기화
for(int i=0; i<array.length; i++){
array[i] = (int)(Math.random()*100);
}
//정렬 하기 전 배열 출력
for(int i=0; i<array.length; i++){
System.out.printf("%d ",array[i]);
if((i+1)%10 == 0){
System.out.println();
}
}
//합병 정렬 함수
merge_sort(array,0,array_length-1);
System.out.println();
System.out.println();
//정렬 후 병열 출력
for(int i=0; i<array.length; i++){
System.out.printf("%d ",array[i]);
if((i+1)%10 == 0){
System.out.println();
}
}
}
다음은 쪼개는 부분입니다.
여기서 [TOP-DOWN]과 [BOTTOM-UP] 방식으로 나눠집니다. 코드를 먼저 보겠습니다.
public static void merge_sort(int[] array, int first, int second){
/*
* 재귀 함수의 경우 무한 루프를 탈 수 있기 때문제 조건부 return을 꼭 걸어줘야 한다.
* 해당 반환은 첫번쨰값과 두번째 값이 같을 때 반환을 하는데
* 이는 서브 리스트 길이가 1임을 의미한다
*/
if(first == second) return;
//반인 인덱스를 찾는 mid 변수
int mid = (first+second)/2;
/*
* 첫번째 값과 mid값(반값)을 재귀 함으로 인데스를 반으로 나눌 수 있게 된다.
* 위에는 왼쪽의 서브 리스트 아래 함수는 오른쪽의 서브 리스트를 의미한다.
*/
merge_sort(array,first,mid);
merge_sort(array,mid+1,second);
/*
* 재귀가 끝나고 merge함수가 실행되었다는 의미는
* 차례되로 반환되어 병합하고 있다는 의미이다.
* 그럼으로 병합 함수를 실행한다.
*/
merge(array,first,mid,second);
}글로 설명하면 어려우니 다음 그림을 함께 보겠습니다.
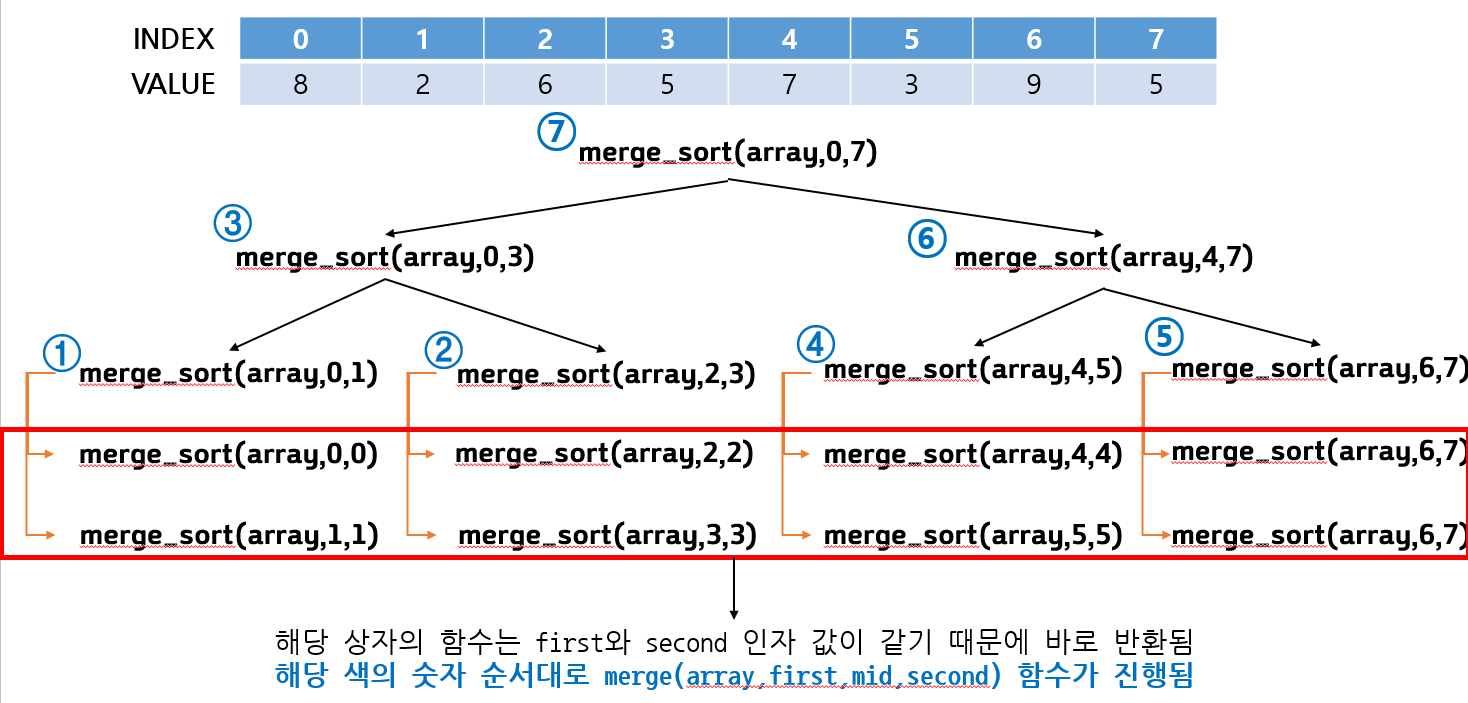
list의 value 값은 여기서는 잠시 무시합시다. 인덱스를 기준으로 이야기 한번 해보겠습니다.
* 해당 순서는 그림의 번호를 이야기하지 않습니다. 순서의 번호를 이야기합니다.
1. merge_sort에 0,7 값이 들어옵니다.
2. 그것을 반으로 쪼개서 위에 함수와 아래 함수로 다시 재귀합니다.
3. 위에는 0,3 아래는 4,7이 들어갑니다. 프로그램 순서상 위에 함수부터 실행됩니다.
4. 0,3을 반으로 쪼개서 위에는 0,1 아래는 2,3이 들어갑니다. 프로그램 순서상 위에서부터 실행됩니다.
5. 0,1을 반으로 쪼개서 위에는 0,0 아래는 1,1 이 들어갑니다. 프로그램 순서상 위에서부터 실행됩니다.
6. 0,0은 조건에 의해 반환됩니다. 프로그램 순서상 아래 함수가 실행됩니다. 1,1 역시 조건에 의해 반환됩니다.
7. 5번으로 돌아가 0,1인 상태에서 아래위에 함수를 모두 실행했으므로 merge(array, first, mid, second) 함수를 실행합니다.
8. 7번 실행이 끝나면 4번으로 올라가 0,3인 상태에서 위에 함수인 0,1이 끝났으므로 2,3을 실행합니다.
9. 2,3을 반으로 쪼개어 2,2와 3,3으로 나눕니다. 2,2와 3,3은 같은 값임으로 반환됩니다.
10. 2,3인 상태로 merge(array, first, mid, second)을 실행합니다.
11. 10번이 끝나면 다시 4번으로 올라갑니다. 0,1과 2,3번의 실행이 끝났으니 0,3의 merge(array, first, mid, second)을 실행합니다.
12. 4번의 실행이 모두 끝났으니 3번으로 올라갑니다. 3번의 4,7을 실행합니다.
.... merge_sort(array,4,7)도 위와 같은 로직을 동일하게 탑니다.
* 혹여나 뒤에 순번이 필요하시면 댓글을 달아주세요.
글로 길게 썼는데 사실 그림으로 보는 것이 훨씬 직관적이고 쉽습니다. 글은 그림으로만 이해가 되지 않을 때 참고하시라고 써놨습니다.
다음은 merge함수 부분입니다.
public static void merge(int[] array, int first, int mid, int second){
int l = first;//왼쪽의 비교할 서브 리스트의 인덱스
int m = mid+1;//오른쪽의 비교할 서브 리스트의 인덱스
int index = first;//비교 한 후 입력할 배열
//외쪽과 오른쪽 둘 중 하나의 서브 리스트의 비교가 끝나면 while문을 종료합니다.
while(l<=mid && m<=second){
//왼쪽 서브리스트와 오른쪽 서브 리스트를 비교하면서 정렬 배열에 입력합니다.
if(array[l] <= array[m]){
sort_array[index] = array[l];
l++;
index++;
}
else{
sort_array[index] = array[m];
m++;
index++;
}
}
/*
* 왼쪽 서브 리스트와 오른쪽 서브 리스트가 정렬 배열에 입력되지 않고 남았을경우
* 이미 서브 리스트는 정렬이 되어 있는 상태임으로 정렬된 리스트 뒤에 붙입니다.
*/
while(l<=mid){
sort_array[index] = array[l];
l++;
index++;
}
while(m<=second){
sort_array[index] = array[m];
m++;
index++;
}
//정렬된 배열의 값을 배열에 입력합니다.
for(int i=first; i<=second; i++){
array[i] = sort_array[i];
}
}merge_sort 함수를 이해하셨다면 merge함수는 어렵지 않으실 겁니다. merge함수는 서브 리스트가 들어왔을 때 중간 mid를 통해 왼쪽 서브 리스트와 오른쪽 서브 리스트로 나눠서 비교하면서 병합하는 함수입니다. 위에 그림과 반대로 아래서부터 병합한다고 생각하시면 좀 더 명확하실 겁니다.
해당 함수는 "왼쪽 서브 리스트의 첫 번째 값, 오른쪽 서브 리스트의 첫 번째 값부터 차례대로 비교하고 비교가 끝난 후 남은 서브 리스트는 뒤에 그냥 붙인다."라고 생각하고 구현하면 좀 더 쉽게 구현하실 수 있으실 겁니다.
[BOTTOM-UP] 전체코드
import java.util.Scanner;
public class Merge_sort {
static int[] sort_array;// 새로운 정렬을 저장할 배열
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
//배열의 길이를 결정
int array_length = sc.nextInt();
int[] array = new int[array_length];//초기 배열
sort_array = new int[array_length];//정렬을 저장할 배열
//배열 초기화
for(int i=0; i<array.length; i++){
array[i] = (int)(Math.random()*100);
}
//정렬 하기 전 배열 출력
for(int i=0; i<array.length; i++){
System.out.printf("%d ",array[i]);
if((i+1)%10 == 0){
System.out.println();
}
}
//합병 정렬 함수
merge_sort(array,0,array_length-1);
System.out.println();
System.out.println();
//정렬 후 병열 출력
for(int i=0; i<array.length; i++){
System.out.printf("%d ",array[i]);
if((i+1)%10 == 0){
System.out.println();
}
}
}
/*
* [BOTTOM-UP] 방식
* 아래서 부터 위로 올라면서 바로 병합하기 때문에 BOTTOM-UP 방식이라고 한다.
* 이중 반복문을 사용해서 list 길이가 1인 것부터 점점 늘려가는 형식의 함수이다.
*/
public static void merge_sort(int[] array, int first, int second){
/*
* list_size을 기준으로 1일때 2일때 4일때.. 배열의 인덱스의 규칙이 같음으로
* 해당 list_size을 기준으로 반복문을 먼저 돌립니다.
* 해당 list_size는 최대값이 전체 배열의 길이를 넘을 수 없음으로 second까지를 최대값으로 설정합니다.*/
for(int list_size = 1; list_size<=second; list_size+=list_size){
/*
* left는 각 서브리스트의 첫번쨰 인덱스를 의미합니다.
* 각 서브리스트의 첫번째 인덱스의 규칙은 left에서 길이의 2배 만큼 더하면 됩니다.
* 그래서 list_size*2를 해줍니다.
* left값은 마지막 인덱스 값보다 커질 수 없습니다.
* 하지만 중간값을 구할 때 outofindex 에러가 날 수 있으니 list_size만큼은 뺴줍니다.
* left는 마지막 서브 리스트의 mid 인덱스 만큼 역시 커질 수 없습니다.*/
for(int left = first; left <= second-list_size; left+=(list_size*2)){
int l = left; // 각 서브 리스트의 첫 번째 값
int r = left + (list_size*2) -1; // 각 서브리스트의 다음 첫 번째 인덱스에서 1일빼서 마지막 인덱스를 구함
int m = left + list_size-1; // left에서 사이즈 만큼 더하면 중간값이 나오게 됩니다. 인덱스는 0부터 시작함으로 -1을 해줍니다.
merge(array,l,m,Math.min(r,second));
}
}
}
public static void merge(int[] array, int first, int mid, int second){
int l = first;//왼쪽의 비교할 서브 리스트의 인덱스
int m = mid+1;//오른쪽의 비교할 서브 리스트의 인덱스
int index = first;//비교 한 후 입력할 배열
//외쪽과 오른쪽 둘 중 하나의 서브 리스트의 비교가 끝나면 while문을 종료합니다.
while(l<=mid && m<=second){
//왼쪽 서브리스트와 오른쪽 서브 리스트를 비교하면서 정렬 배열에 입력합니다.
if(array[l] <= array[m]){
sort_array[index] = array[l];
l++;
index++;
}
else{
sort_array[index] = array[m];
m++;
index++;
}
}
/*
* 왼쪽 서브 리스트와 오른쪽 서브 리스트가 정렬 배열에 입력되지 않고 남았을경우
* 이미 서브 리스트는 정렬이 되어 있는 상태임으로 정렬된 리스트 뒤에 붙입니다.
*/
while(l<=mid){
sort_array[index] = array[l];
l++;
index++;
}
while(m<=second){
sort_array[index] = array[m];
m++;
index++;
}
//정렬된 배열의 값을 배열에 입력합니다.
for(int i=first; i<=second; i++){
array[i] = sort_array[i];
}
}
}
그럼 바뀐 코드 부분을 자세히 살펴보겠습니다.
바뀐 코드는 merge_sort함수 부분입니다.
public static void merge_sort(int[] array, int first, int second){
/*
* list_size을 기준으로 1일때 2일때 4일때.. 배열의 인덱스의 규칙이 같음으로
* 해당 list_size을 기준으로 반복문을 먼저 돌립니다.
* 해당 list_size는 최대값이 전체 배열의 길이를 넘을 수 없음으로 second까지를 최대값으로 설정합니다.*/
for(int list_size = 1; list_size<=second; list_size+=list_size){
/*
* left는 각 서브리스트의 첫번쨰 인덱스를 의미합니다.
* 각 서브리스트의 첫번째 인덱스의 규칙은 left에서 길이의 2배 만큼 더하면 됩니다.
* 그래서 list_size*2를 해줍니다.
* left값은 마지막 인덱스 값보다 커질 수 없습니다.
* 하지만 중간값을 구할 때 outofindex 에러가 날 수 있으니 list_size만큼은 뺴줍니다.
* left는 마지막 서브 리스트의 mid 인덱스 만큼 역시 커질 수 없습니다.*/
for(int left = first; left <= second-list_size; left+=(list_size*2)){
int l = left; // 각 서브 리스트의 첫 번째 값
int r = left + (list_size*2) -1; // 각 서브리스트의 다음 첫 번째 인덱스에서 1일빼서 마지막 인덱스를 구함
int m = left + list_size-1; // left에서 사이즈 만큼 더하면 중간값이 나오게 됩니다. 인덱스는 0부터 시작함으로 -1을 해줍니다.
merge(array,l,m,Math.min(r,second));
}
}
}사실 6줄 정도의 코드지만 굉장히 어렵습니다.
3가지 순서로 설명하겠습니다.
1. 각 반복문의 시작값지정, 조건식, 증감식을 어떻게 구하게 되었는가
2. 각 변수를 지정하는 수식의 이유
3. 코드를 진행하면서 나올 수 있는 의문들
1. 각 반복문의 시작값지정, 조건식, 증감식을 어떻게 구하게 되었는가
첫 번째 반복문의 경우 list_size라는 변수를 설정했습니다.
조금 다른 이야기지만 정렬 알고리즘에서 재귀형식은 지양하는 편입니다.
그래서 반복문을 사용해서 문제를 해결하면 best인데 어떻게 반복문을 사용할 것인가를 생각해 보면
가장 먼저 보이는 규칙이 서브 리스트의 길이입니다.
서브 리스트가 1인 리스트부터 2,4,8 리스트로 길이가 늘어납니다.
각 서브 리스트의 길이에 따라 서브리스트의 인덱스 첫 값, 중간값, 마지막값의 규칙이 동일합니다.
그래서 일단 첫 번째 반복문은 서브 리스트의 길이로 만들어 줍니다.
두 번째 반복문의 경우는 실제로 서브 리스트의 값을 구해야 합니다.
그래서 서브리스트의 첫 번째 값을 구하는 게 중요합니다.
여기서 잘 생각해야 하는게 서브 리스트의 길이가 1일 때는 비교하면서 합칠 필요가 없습니다. 서브 리스트가 1인 길이라고 코드는 진행하고 있지만 사실 1인 길이를 2로 합치는 과정인 것이지요. 그러면 결국에는 서브 리스트의 첫 번째 인덱스는 1일 때는 2만큼 2일 때는 4만큼 4일 때는 8만큼 차이가 나는 것입니다.
그래서 증가값을 list*2로 한 것입니다. 사실은 2배만큼 차이 난 결과를 가져와야 하는 것이니깐요.
*이해가 잘 안 되실 수 있습니다. 댓글로 달아주시면 더 상세하게 답변해 드리겠습니다.
left는 해당 중간인덱스 이상을 넘어갈 수 없습니다. 그래서 조건식을 second-list_size를 한 것입니다.
왜 마지막 서브 리스트의 중간인덱스가 second-list_size 인지는 2번에서 말씀드리겠습니다.
2. 각 변수를 지정하는 수식의 이유
l이 left인 것은 위에 설명을 이해하셨다면 어렵지 않을 것입니다.
m이 left+list_size-1인 이유는 생각해 보면 간단합니다. 다음 서브 리스트의 첫 번째 인덱스가 list_size*2입니다. 그럼 그것의 반만큼만 더해주면 중간값이 나오는 것이죠. 그래서 마지막 중간값 역시 second(마지막 인덱스)에서 list_size을 뺀 값이 되는 것입니다. r은 마지막 서브리스트의 마지막 인덱스입니다. 다음 서브 리스트의 첫 번째 인덱스에서 1을 빼주면 마지막 인덱스 값이 나오겠죠.
함수에서는 r이 마지막 인덱스를 벗어날 수 있음으로 최댓값을 마지막 인덱스로 설정해 줍시다.
3. 코드를 진행하면서 나올 수 있는 의문들
Q1) 서브리스 길이를 처음부터 2로 설정하고 하면 안 되나요?
그래도 됩니다. 대신 list_size을 더하거나 빼는 모든 부분 m을 구하는 부분을 2로 나눠주셔야 하고 m값이 인덱스를 초과할 수 있음으로 최소값 처리를 해주셔야 합니다.
Q2) 왜 m을 (l+r)/2로 구하지 않는 건가요? 중간 값인데요?
사실 한번 해보시면 아는데 정확하게 반으로 쪼개지지 않는 리스트 길이가 있기 때문입니다.
예를 들어 리스트 길이가 9인 인덱스가 있다고 해봅시다. 그림을 보겠습니다.
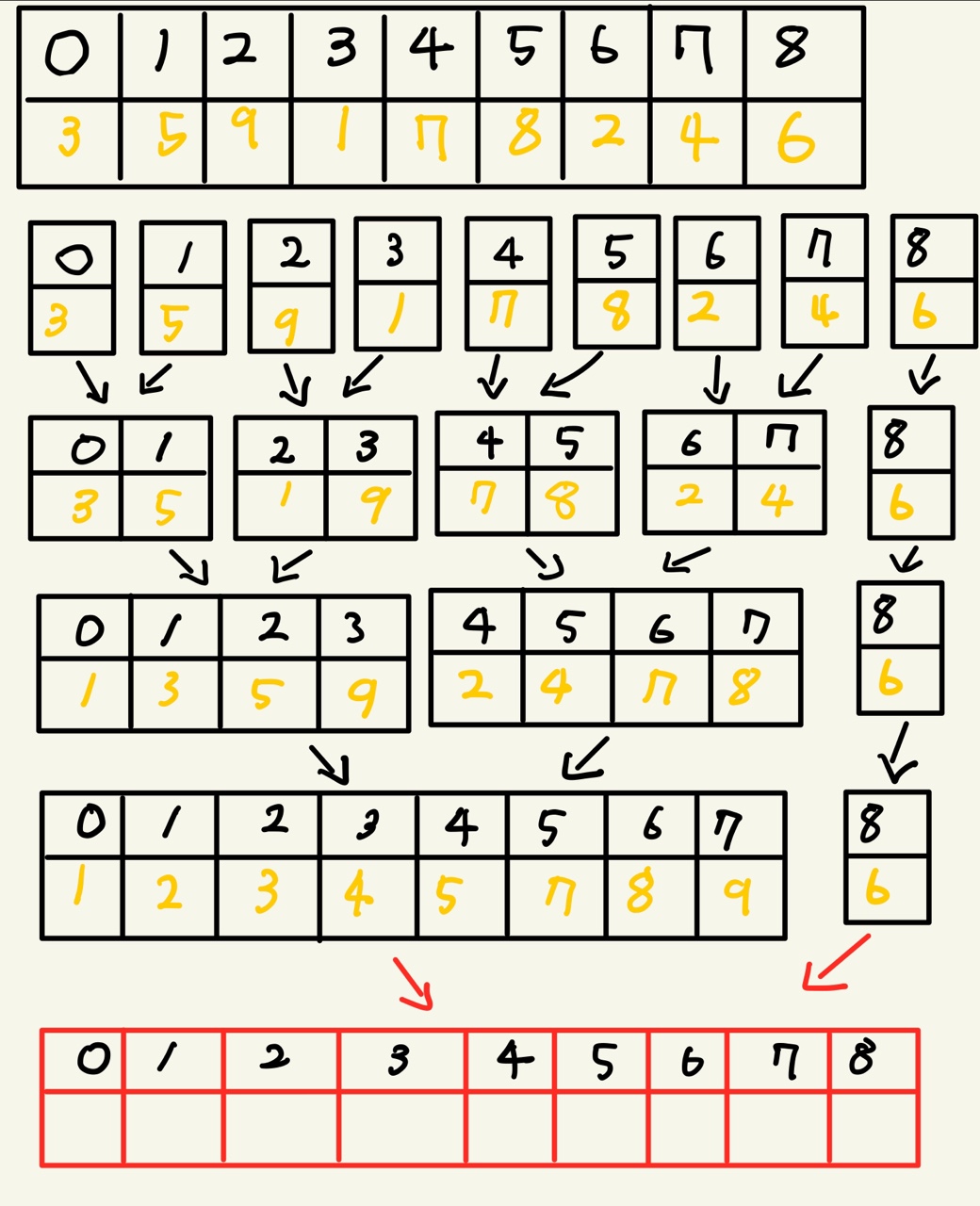
마지막만 보시면 됩니다. 마지막을 보시면 [0,1,2,3,4,5,6,7] 인덱스와 [8] 인덱스가 합쳐질 타이밍입니다.
그렇게 되면 merge함수에서 합쳐지겠죠 그렇다면 (l+r)/2 -1을 하게 되면 어떻게 될까요 merge(array,0,3,8) 이런 식으로 매개변수가 넘어가게 됩니다. 그렇게 되면 m이 3 임으로 비교하는 구간이 인덱스 0과 4입니다. 근데 0과 4는 이미 정렬이 된 인덱스입니다. [0,4], [1,4], [2,4], [3,4] 이렇게 비교하게 될 것입니다. 0,1,2,3은 4보다 크지 않으니깐요 그렇게 되면 모든 인덱스가 정렬이 된 것으로 보고 로직에서는 3 인덱스 뒤에 4,5,6,7,8을 붙이게 될 것입니다. 그러면 마지막 인덱스 8이 정렬이 되지 않고 [1,2,3,4,5,6,7,8,9,6] 이런 식으로 결과 값이 나오게 될 것입니다.
그렇다면 어떻게 마지막 인덱스를 정렬할 수 있을까요? 바로 0과 8을 비교하는 것입니다. 그렇게 차례대로 비교하다 보면 인덱스 8이 들어가야 할 부분을 찾아 들어갈 수 있게 됩니다. 그렇게 되려면 m이 7이 되어야 합니다. 그렇게 되려면 list_size인 8을 더하고 1을 빼주면 해당 수를 구할 수 있게 됩니다. 즉 다음 배열이 16개가 있다고 가정하고 m을 구해야 올바른 정렬을 할 수 있는 것입니다.
5. 병합정렬 알고리즘 장단점
마지막으로 이 배열의 장점과 단점을 기록하겠습니다.
해당 알고리즘이 어떤 부분에서 좋고 어떤 상황에 쓰면 되는지에 관한 내용입니다.
장점
1. 항상 두 부분리스트로 쪼개어 들어가기 때문에 최악의 경우에도 시간 복잡도가 O(NlogN)으로 유지가 된다.
2. 안정정렬이다.
단점
1. 정렬과정에서 추가적인 보조 배열 공간을 사용하기 때문에 메모리 사용량이 많다.
2. 보조 배열에서 원본배열로 복사하는 과정은 매우 많은 시간을 소비하기 때문에 데이터가 많을 경우 상대적으로 시간이 많이 소요된다.
시간복잡도에 관한 이야기는 다음에 해보도록 하겠습니다.
다음 블로그를 참고하여 작성한 글입니다.
https://st-lab.tistory.com/233
자바 [JAVA] - 합병정렬 / 병합정렬 (Merge Sort)
[정렬 알고리즘 모음] 더보기 1. 계수 정렬 (Counting Sort) 2. 선택 정렬 (Selection Sort) 3. 삽입 정렬 (Insertion Sort) 4. 거품 정렬 (Bubble Sort) 5. 셸 정렬 (Shell Sort) 6. 힙 정렬 (Heap Sort) 7. 합병(병합) 정렬 (Merge
st-lab.tistory.com
'알고리즘 > Java_정렬_알고리즘' 카테고리의 다른 글
| 자바로 구현한 카운팅 정렬(Counting Sort/계수 정렬) 알고리즘 (0) | 2023.03.02 |
|---|---|
| 자바로 구현한 셀 정렬(Shell Sort) 알고리즘 (0) | 2023.02.23 |
| 자바로 구현한 버블 정렬(거품 정렬) 알고리즘 (0) | 2023.02.22 |
| 자바로 구현한 삽입 정렬 알고리즘 (0) | 2023.02.20 |
| 자바로 구현한 선택 정렬 알고리즘 (0) | 2023.02.20 |